Linear functions are trivial to solve, as are quadratic functions if you memorize the quadratic formula. However, polynomials of higher degrees and non-polynomial functions are much more difficult to solve. The simplest technique for solving these types of equations is to use an iterative root-finding technique.
We will try out the following techniques using the function:
$$f(x) = x^3 -x -1$$
Graph of the equation for further outcome validation:
There are several methods to find the root of the polynomial equations. They are-
Bisection method,
False position method,
Newton-Raphson method,
Secant method and
Newton's Method
Bisection Method
The bisection method is the simplest root-finding technique. The algorithm for bisection is similar to binary search. To use this method, we need to know about the intermediate value theorem (if f is a continuous function whose domain contains the interval [a, b], then it takes on any given value between f(a) and f(b) at some point within the interval). One of the outcomes of this theorem is "If a continuous function has values of opposite sign inside an interval, then it has a root in that interval" (Bolzano's theorem)
Algorithms for Bisection Method:
1. start
2. Define function f(x)
3. Choose initial guesses 'x0' and 'x1' such that f('x0')f('x1') < 0
4. Choose pre-specified tolerable error 'e'.
5. Calculate new approximated root as 'x2' = ('x0' + 'x1')/2
6. Calculate f('x0')f('x2')
a. if f('x0')f('x2') < 0 then 'x1' = 'x2'
b. if f('x0')f('x2') > 0 then 'x0' = 'x2'
c. if f('x0')f('x2') = 0 then goto (8)
7. if |f('x2')| > 'e' then goto (5) otherwise goto (8)
8. Display 'x2' as root.
9. Stop
Code for Bisection Method in C++:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
double F (double x) {
// define the polynomial function here
return x*x*x -x - 1;
}
// Showing Each Iteration Function
void draw(vector<double>& v) {
cout << "id\t\tx1\t\tx2\t\tx3\n";
for (int i = 0; i < v.size()/3; i++) {
cout << i+1 << "\t\t" << setprecision(4) << v[3*i] << "\t\t" << setprecision(4) << v[3*i+1] << "\t\t" << setprecision(4) << v[3*i+2] << '\n';
}
}
void solve () {
double x1,x2;
cin >> x1 >> x2;
if (F(x1) * F(x2) > 0) {
cout << "No solution\n";
return;
}
double E = 0.0001;
double x3 = (x1+x2)/2;
vector<double> v;
while (abs(F(x3)) > E) {
x3 = (x1+x2)/2;
if (F(x1) * F(x3) < 0) x2 = x3;
else x1 = x3;
v.pb(x1);
v.pb(x2);
v.pb(x3);
}
cout << x3 << '\n';
draw(v);
}
int main () {
solve();
return 0;
}
The output of the program:
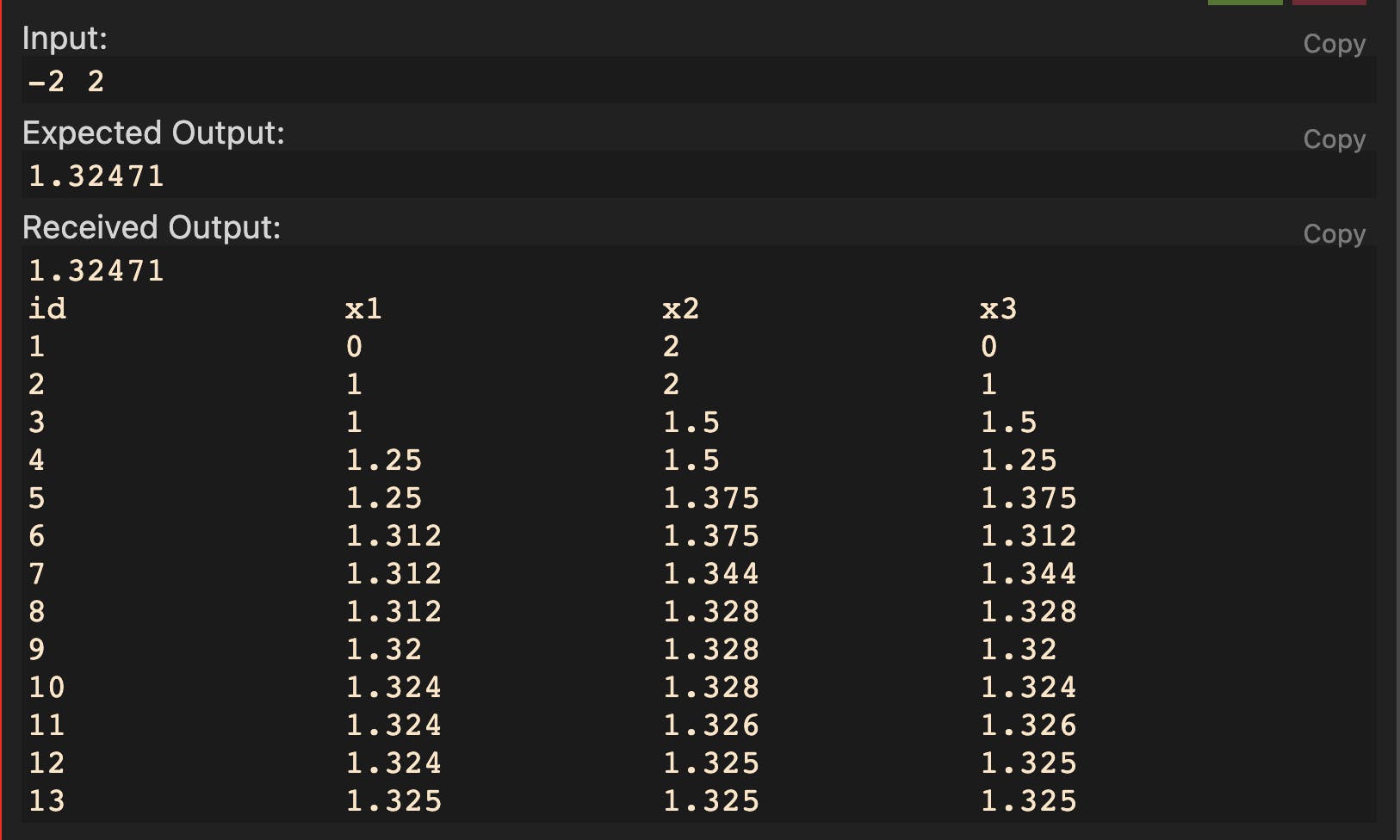
Convergence
The bisection method has linear convergence with a constant of 1/2.
Drawbacks
The bisection method cannot solve for the root of x², as it never becomes negative.
False Position Method
The False position method works on the principle of the x-interception (C,0) of the straight line between two (x1, f(x1) ) and (x2, f(x2) ) points.
We know the the slope of straight line A { (x1, f(x1) ), (x2, f(x2) ) } and straight line B { ( (x1, f(x1) ), (C, f(C) ) or (x2, f(x2)) , (C, f(C) ) ) } is same.
$$\dfrac{f(x2)-f(x1)}{x2-x1} = \dfrac{0-f(x1)}{C-x1}$$
$$\therefore C = x1 - \dfrac{(x2-x1)*f(x1)}{f(x2)-f(x1)}$$
Visual representation of moving to the closer of the root of the equation by one of the iterations:
The working procedure is the same as the bisection method except for the approximate root formula.
Algorithm for False Position method:
1. start
2. Define function f(x)
3. Choose initial guesses 'x0' and 'x1' such that f('x0')f('x1') < 0
4. Choose pre-specified tolerable error 'e'.
5. Calculate new approximated root as 'x2' = = 'x0'- (f('x0') ('x1'-'x0') ) / (f ('x1') – f ('x0'))
6. Calculate f('x0')f('x2')
a. if f('x0')f('x2') < 0 then 'x1' = 'x2'
b. if f('x0')f('x2') > 0 then 'x0' = 'x2'
c. if f('x0')f('x2') = 0 then goto (8)
7. if |f('x2')| > 'e' then goto (5) otherwise goto (8)
8. Display 'x2' as root.
9. Stop
Code for false position method in C++:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
double F (double x) {
// define the polynomial function here
return x*x*x -x - 1;
}
// Showing Each Iteration Function
void draw(vector<double>& v) {
cout << "id\t\tx1\t\tx2\t\tx3\n";
for (int i = 0; i < v.size()/3; i++) {
cout << i+1 << "\t\t" << setprecision(4) << v[3*i] << "\t\t" << setprecision(4) << v[3*i+1] << "\t\t" << setprecision(4) << v[3*i+2] << '\n';
}
}
void solve () {
double x1,x2;
cin >> x1 >> x2;
if (F(x1) * F(x2) > 0) {
cout << "No solution\n";
return;
}
double E = 0.0001;
double x3 = (x1+x2)/2;
vector<double> v;
while (abs(F(x3)) > E) {
x3 = x1- (F(x1) * (x2-x1) ) / (F (x2) - F (x1));
if (F(x1) * F(x3) < 0) x2 = x3;
else x1 = x3;
v.pb(x1);
v.pb(x2);
v.pb(x3);
}
cout << x3 << '\n';
draw(v);
}
int main () {
solve();
return 0;
}
The output of the program:
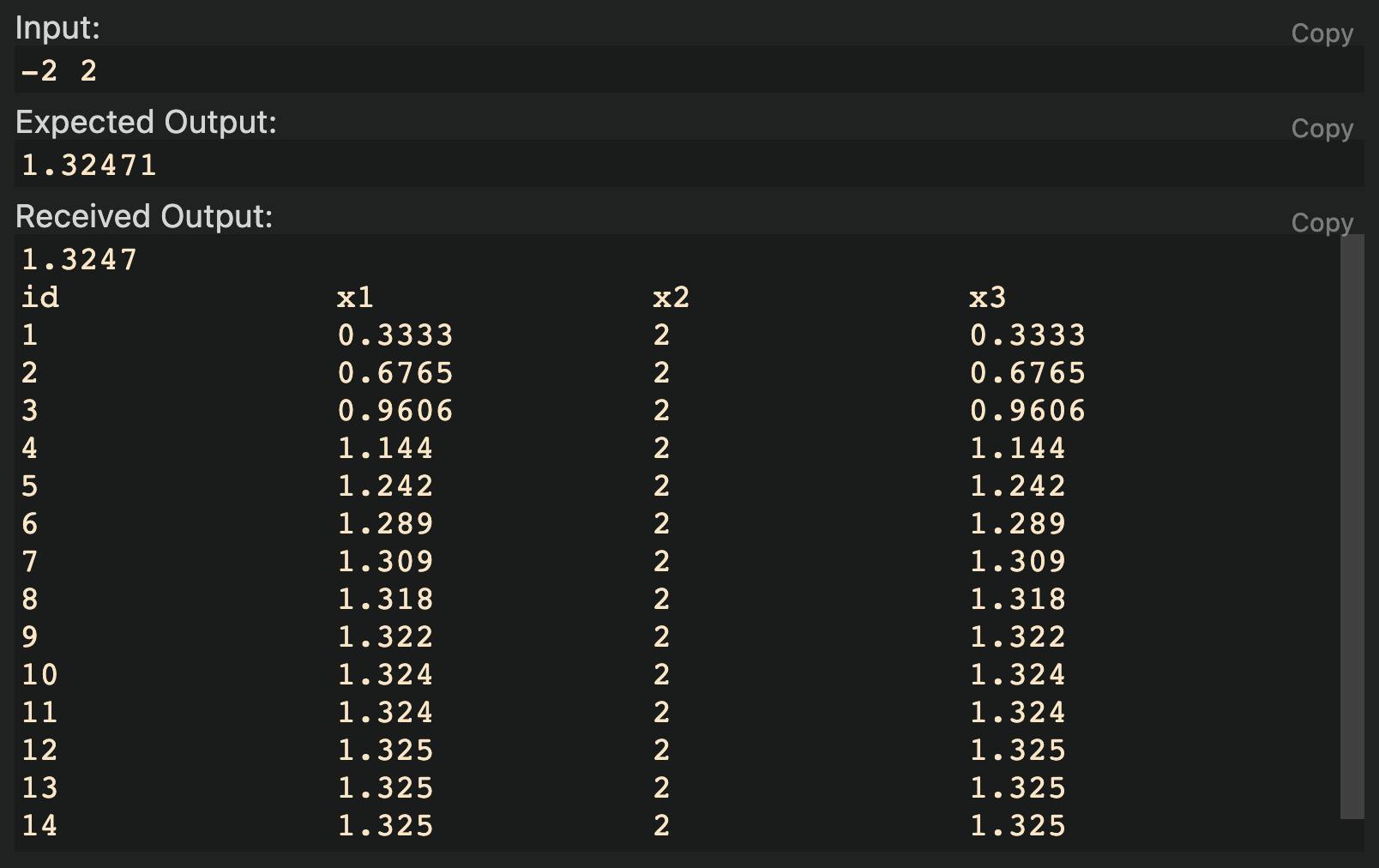
Convergence:
The rate of convergence may vary widely depending on the function and the initial interval used.
Drawbacks:
Potential for oscillations: In some cases, the false position method can oscillate between two endpoints without converging to the root. This can happen when the function has a steep gradient near the root.
The Newton-Raphson Method
Newton-Raphson's method is based on the working principle of function derivatives because it updates the approximate root variable with the y-axis-intercept value of the tangent of the equation that touches the previous approximate root value.
The visual representation of Newton-Raphson's Method:
To use this method, we require an initial guess and the 1st derivatives of the function so that we can form a tangent line and update the approximate value closer to the root.
$$y - F(X_{n-1}) = F'(X_{n-1})* (X_{n}- X_{n-1})$$
$$\therefore X_{n} = X_{n-1} - \dfrac{F(X_{n-1})}{F'(X_{n-1})}$$
Algorithm for Newton-Raphson's Method:
1. Start
2. Define the F(x)
3. Define the derivative of the F1(x)
4. Choose pre-specified tolerable error 'e'.
6. Set initial variable 'x0' via input
6. While function(x0) > 'e':
7. 'x0' = 'x0' - F('x0')/F1('x0')
8. Display 'x0' as root
9. Stop
Code for Newton-Raphson's Method in C++:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
double F (double x) {
// define the polynomial function here
return x*x*x -x - 1;
}
double F1 (double x) {
// define the derivative of the polynomial function here
return 3*x*x - 1;
}
// Showing Each Iteration Function
void draw(vector<double>& v) {
cout << "id\t\tXn\n";
for (int i = 0; i < v.size(); i++) {
cout << i+1 << "\t\t" << setprecision(4) << v[i] << '\n';
}
}
void solve () {
double x0;
cin >> x0;
double E = 0.0001;
vector<double> v;
while (abs(F(x0)) > E) {
x0 = x0 - F(x0)/F1(x0);
v.pb(x0);
}
cout << x0 << '\n';
draw(v);
}
int main () {
solve();
return 0;
}
The output of the program:
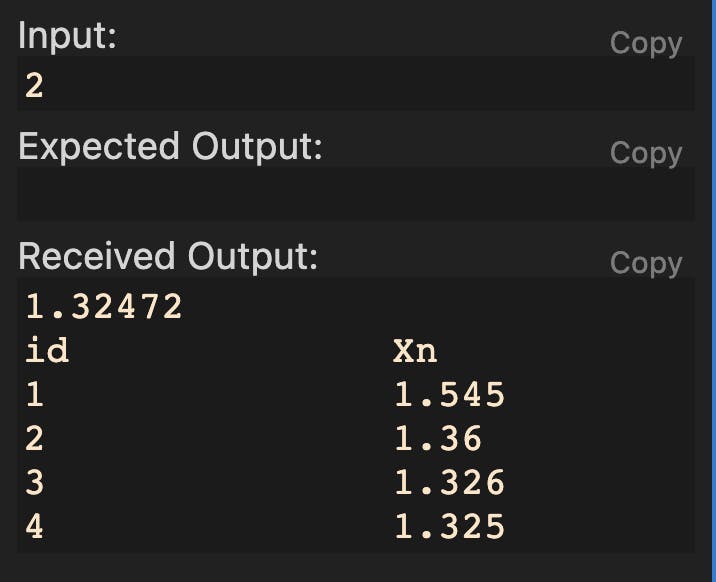
Convergence:
This rapid convergence makes Newton-Raphson's method one of the most popular algorithms for finding roots of nonlinear equations.
Drawbacks:
Sensitivity to initial guess: Newton-Raphson's method requires an initial guess of the root. If the initial guess is not close enough to the actual root, the method may fail to converge, converge to the wrong root, or oscillate between different roots. In practice, finding an appropriate initial guess can be difficult, especially when dealing with complex functions.
Need for derivative information: Newton-Raphson's method requires the derivative of the function to be evaluated at each iteration. This can be computationally expensive, especially when the function is complex or expensive to evaluate. Additionally, the derivative may not be readily available or may be difficult to compute accurately.
Potential for divergence: Newton-Raphson's method can diverge if the derivative of the function is close to zero or if it changes sign in the neighborhood of the root. This can happen when the function has singularities or sharp turns near the root.
Not guaranteed to converge: Newton-Raphson's method is not guaranteed to converge to a root in all cases. For example, if the function has an infinite number of roots or if the initial guess is very far from the root, the method may not converge.
Multiple roots: If the function has multiple roots that are close together, Newton-Raphson's method may converge to a root that is different from the desired one. This can happen if the initial guess is not sufficiently accurate.
Requires smoothness of the function: Newton-Raphson's method requires the function to be differentiable and smooth in the neighborhood of the root. If the function has discontinuities, singularities, or sharp turns near the root, the method may fail to converge or converge very slowly.
Secant Method
secant method uses the same technique as Newton-Raphson's Method. But sometimes, it's hard to find the derivative of the function analytically. The Secant method overcomes this problem by using the estimating value of the tangent's slope / derivative function.
$$F'(X_{n-1}) \approx \dfrac{ F(X_{n-1}) - F(X_{n-2})}{X_{n-1}-X_{n-2}}$$
$$X_{n} = X_{n-1} - \dfrac{F(X_{n-1}) * (X_{n-1} - X_{n-2})}{F(X_{n-1}) - F(X_{n-2})}$$
$$X_{n} = \dfrac{X_{n-2} * F(X_{n-1}) - X_{n-1} * F(X_{n-2})}{F(X_{n-1}) - F(X_{n-2})}$$
In short, we can use this formula to compute the result
$$\therefore X_3 = \dfrac{x_1F_2 - x_2F_1}{F_2 - F_1}$$
Code for secant method in C++:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
double F (double x) {
// define the polynomial function here
return x*x*x -x - 1;
}
// Showing Each Iteration Function
void draw(vector<double>& v) {
cout << "id\t\tXn\n";
for (int i = 0; i < v.size(); i++) {
cout << i+1 << "\t\t" << setprecision(4) << v[i] << '\n';
}
}
void solve () {
double x1,x2;
cin >> x1 >> x2;
double E = 0.0001;
double f1, f2;
f1 = F(x1);
f2 = F(x2);
double x3 = x1;
vector<double> v;
while (abs(F(x3)) > E) {
x3 = (x1*f2 - x2*f1)/ (f2-f1);
x1 = x2;
x2 = x3;
f1 = F(x1);
f2 = F(x2);
v.pb(x3);
}
cout << x3 << '\n';
draw(v);
}
int main () {
solve();
return 0;
}
The output of the program:
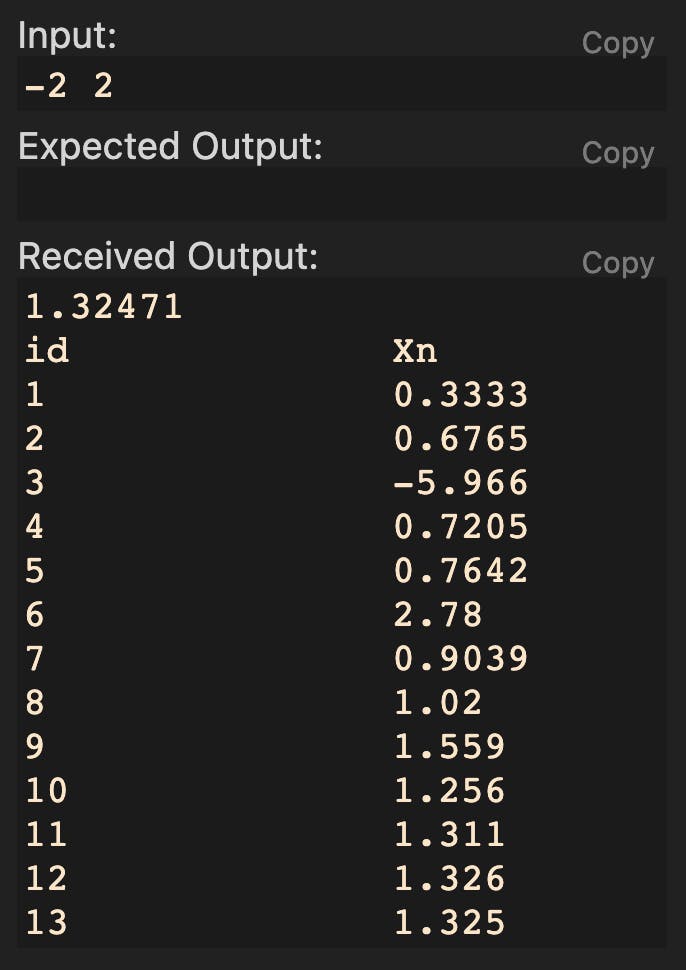
Convergence:
This method has slower convergence than Newton-Raphson's Method.
Drawbacks:
Same drawbacks as Newton-Raphson's method, except you don't need to find out the derivative of the function.
N.B: Newton's and Modified Bi-section methods are coming soon on this post.
Practice Questions:
Write a program on the function f(x) = 2x³ + 3x - 1 to output all the possible real roots of the function with a tolerance of 0.0001.
Write a program on the function f(x) = x³ + 9x - 4 with a tolerance of 0.001 to find the root of the function and decide which methods will perform better.

